NEET - 2015

HOME >> NEET - 2015

Welcome Dear Student and Shine in NEET with Shine NEET SmartPrep!.
All NEET - 2015 questions are displayed here. But you would be able to try only a sub set of these questions in your free trial.
We recommend you explore the full system and go for a one time subscription if you are satisfied.
Try it out and feel the difference!!

Subscribe to full version of smart test prep solution for the same cost of a static and boring printed question bank!

Limited-Time Offer: Get all this for just ₹1199

Why settle for outdated methods when you can prepare smarter, track better, and score higher?
Subscribe Now & Take Control of Your NEET Prep !

Your Full Test Performance Summary

You are yet to try out this test. Performance Summary not avialable !

Questions Available: 66

Questions Attempted: 0

Number of Attempts: 0

Correct Attempts: 0

Total Time Spent: 00:00

Avg Time Per Question: 00:00

Start Test

1. If dimensions of critical velocity v_c of a liquid flowing through a tube areexpressed as [η^xρ^yγ^z] where η, ρ and γ are the coefficient of viscosity of liquid, density of liquid and radius of the tube respectively, then the values of x, y and z are given by.

(1). -1,-1,-1

(2). 1,1,1

(3). 1,-1,-1

(4). -1,-1,1

2. A particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v(x) = βx⁻²ⁿ, where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x is given by

(1). −2β²x^{−2n + 1}

(2). −2nβ²e^{−4n + 1}

(3). −2nβ²x^{−2n − 1}

(4). −2nβ²x^{−4n − 1}

3. If vectors \(\vec{A}\) = cos wt \(\hat{i}\) + sin wt\(\hat{j}\) and \(\vec{B}\) = cos \(\frac{wt}{2} \hat{i}\) + sin wt\(\hat{j}\) are functions of time, then the value of t at which they are orthogonal to each other is

(1). t = \( \frac{ \pi }{2}\)

(2). t = 0

(3). \( \frac{\pi } {4w}\)

(4). t = \( \frac{\pi } {2w}\)

4. The position vector of a particle \(\vec{R}\) as a function of time is given by \(\vec{R}\) = 4 sin\( \left(2\pi t\right)\hat{i}\) + 4 cos\( \left(2\pi t\right)\hat{j}\). Where R is in meters, t is in seconds and \(\hat{i}\) and \(\hat{j}\) denotes unit vectors along x - and y - directions, respectively. Which one of the following statements is wrong for the motion of particle

(1). Magnitude of velocity of particle is 8 metre/second

(2). Path of the particle is a circle of radius 4 metre

(3). Acceleration vector is along - \(\vec{R}\)

(4). Magnitude of acceleration vector is \(\frac{V^2}{R}\), where V is the velocity of particle

5. A ship A is moving westwards with a speed of 10 km\(h^{-1}\) and a ship B 100 km south of A, is moving northwards with a speed of 10 km\(h^{-1}\). The time after which the distance between them becomes shortest, is

(1). 5\(\sqrt{2}\) h

(2). 10\(\sqrt{2}\) h

(3). 0

(4). 5 h

6. Two stones of masses m and 2m are whirled in horizontal circles, theheavier one in a radius r2and the lighter one in radius r. The tangentialspeed of lighter stone is n times that of the value of heavier stone whenthey experience same centripetal forces. The value of n is

(1). 4

(2). 1

(3). 2

(4). 3

7. A plank with a box on it at one end is gradually raised about the otherend. As the angle of inclination with the horizontal reaches 30°, the box starts to slip and slides 4.0 m down the plank in 4.0 s. The coefficients of static and kinetic friction between the box and the plank will be,respectively

(1). 0.5 and 0.6

(2). 0.4 and 0.3

(3). 0.6 and 0.6

(4). 0.6 and 0.5

8. A block A of mass m1 rests on a horizontal table. A light stringconnected to it passes over a frictionless pully at the edge of table andfrom its other end another block B of mass m2 is suspended. Thecoefficient of kinetic friction between the block and the table is μk.When the block A is sliding on the table, the tension in the string is

(1). \(\frac{m_1m_2\left(1 +\mu_k\right)g}{\left(m_1 + m_2\right)}\)

(2). \(\frac{m_1m_2\left(1 − /mu_k\right)}{g\left(m_1 + m_2\right)}\)

(3). \(\frac{\left(m_2 + μ_km_1\right)}{g\left(m_1 + m_2\right)}\)

(4). \(\frac{\left(m_2 − μ_km_1\right)}{g\left(m_1 + m_2\right)}\)

9. Two particles A and B, move with constant velocities \(\vec{v_1}\) and \(\vec{v_2}\).At the initial moment their position vectors are \(\vec{r_1}\) and \(\vec{r_2}\) respectively. Thecondition for particles A and B for their collision is

(1). \(\vec{r_1}\) × \(\vec{v_1}\) = \(\vec{r_2}\) ×\(\vec{v_2}\)

(2). \(\vec{r_1}\) −\(\vec{r_2}\) =\(\vec{v_1}\) −\(\vec{v_2}\)

(3). \(\frac{\vec{r_1} −\vec{r_2}}{|\vec{r_1} −\vec{r_2}|}\)=\(\frac{\vec{v_2} −\vec{v_1}}{|\vec{v_2} −\vec{v_1}|}\)

(4). \(\vec{r_1}\) . \(\vec{v_1}\) = \(\vec{r_2}\) .\(\vec{v_2}\)

10. The heart of a man pumps 5 litres of blood through the arteries per minute at a pressure of 150 mm of mercury. If the density of mercury be13. × 10³kgm³ and g = 10ms² then the power of heart in watt is

(1). 3.0

(2). 1.50

(3). 1.70

(4). 2.35

11. A ball is thrown vertically downwards from a height of 20 m with an initial velocity v₀.It collides with the ground, loses 50 percent of its energy in collision and rebounds to the same height. The initial velocity v₀ is (Take g = 10ms⁻²)

(1). 28 ms⁻¹

(2). 10 ms⁻¹

(3). 14 ms⁻¹

(4). 20 ms⁻¹

12. On a frictionless surface, a block of mass M moving at speed v collides elastically with another block of same mass M which is initially at rest. After collision the first block moves at an angle 0 to its initial direction and has a speed v/3. The second block's speed after the collision

(1). \(\frac{3}{\sqrt{2}}\)v

(2). \(\frac{\sqrt{3}}{2}\)v

(3). \(\frac{2\sqrt{2}}{3}\)v

(4). \(\frac{3}{4}\)v

13. A particle of mass m is driven by a machine that delivers a constantpower k watts. If the particle starts from rest the force on the particle attime t is

(1). \({\sqrt{2mkt}}^{\frac{−1}{2}}\)

(2). \(\frac{1}{2}{\sqrt{mkt}}^{\frac{-1}{2}}\)

(3). \({\sqrt{\frac{mk}{2}t}}^{\frac{−1}{2}}\)

(4). \({\sqrt{mkt}}^{\frac{−1}{2}}\)

14. Two particles of masses m₁, m₂ move with initial velocities u₁ and u₂.On collision, one of the particles get excited to higher level, after absorbing energy e. If final velocities of particles be v₁ and v₂ then we must have

(1). \(\frac{1}{2}m_1{u_1}^2\) + \(\frac{1}{2}m_2{u_2}^2\) - \(\varepsilon\) = \(\frac{1}{2}m_1{v_1}^2\) + \(\frac{1}{2}m_2{v_2}^2\)

(2). \(\frac{1}{2}{m_1}^2{u_1}^2\) + \(\frac{1}{2}m_2{u_2}^2\) -+\(\varepsilon\) = \(\frac{1}{2}{m_1}^2{v_1}^2\) + \(\frac{1}{2}{m_2}^2{v_2}^2\)

(3). \({m_1}^2{u_1}\) + \({m_2}^2{u_2}\) - \(\varepsilon\) = \({m_1}^2{v_1}\) + \({m_2}^2{v_2}\)

(4). \(\frac{1}{2}m_1{u_1}^2\) + \(\frac{1}{2}m_2{u_2}^2\) = \(\frac{1}{2}m_1{v_1}^2\) + \(\frac{1}{2}m_2{v_2}^2\) - \(\varepsilon\)

15. Two similar springs P and Q have spring constants K_P and K_Q such that K_P > K_Q. They are stretched first by the same amount (case a),then by the same force (case b). The work done by the springs W_P and W_Q are related as, in case (a) and case (b) respectively

(1). W_P > W_Q; W_Q > W_P

(2). W_P < W_Q; W _Q< W_P

(3). W_P = W_Q; W_P > W_Q

(4). W_P = W_Q; W_P = W_Q

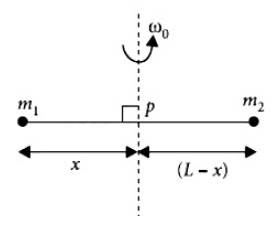
16. Point masses m₁ and m₂ are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ω₀ is minimum, is given by

(1). x = \(\frac{m_2}{m_1}\)L

(2). x = \(\frac{m_2L}{m_1 + m_2}\)

(3). x = \(\frac{m_1L}{m_1 + m_2}\)

(4). x = \(\frac{m_1}{m_2}\)L

17. An automobile moves on a road with a speed of 54 kmh⁻¹.The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kgm². If the vehicle is brought to rest in 15 S, the magnitude of average torque transmitted by its brakes to the wheel is

(1). 10.86 kgm²s⁻²

(2). 2.86 kgm²s⁻²

(3). 6.66 kgm²s−2

(4). 8.58 kgm²s⁻²

18. A force \(\vec{F} = α\hat{i} + 3\hat{j} + 6\hat{k}\) is acting at a point \(\vec{r} = 2\hat{i} − 6\hat{j} − 12\hat{k}\).The value of α for which angular momentum about origin is conserved is

(1). zero

(2). 1

(3). -1

(4). 2

19. A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A.The normal reaction on A is

(1). \(\frac{W (d − x)}{x}\)

(2). \(\frac{W (d − x)}{d}\)

(3). \(\frac{Wx}{d}\)

(4). \(\frac{Wd}{x}\)

20. A mass m moves in a circle on a smooth horizontal plane with velocity v₀ at a radius R₀.The mass is attached to a string which passes through a smooth hole in the plane as shown.The tension in the string is increased gradually and finally m moves in a circle of radius R_o/2.The final value of the kinetic energy is

(1). \(2m{v_0}^2\)

(2). \(\frac{1}{2}m{v_0}^2 \)

(3). \(m{v_0}^2\)

(4). \(\frac{1}{4}m{v_0}^2\)

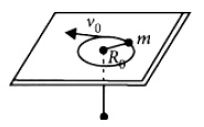
21. Three identical spherical shells, each of mass m and radius r are placed as shown in figure. Consider an axis X X ' which is touching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about X X ' axis is

(1). \(\frac{16}{5}\)mr2

(2). 4mr2

(3). \(\frac{11}{5}\)mr2

(4). 3mr2

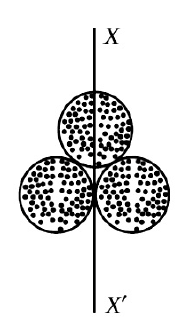
22. The cylindrical tube of a spray pump has radius \(R\), one end of which has n fine holes, each of radius \(r\). If the speed of the liquid in the tube is \(V\),the speed of the ejection of the liquid through the holes is

(1). \(\frac{VR^2}{n^3r^2}\)

(2). \(\frac{V^2R}{nr}\)

(3). \(\frac{VR^2}{n^2r^2}\)

(4). \(\frac{VR^2}{nr^2}\)

23. Water rises to a height \(h\) in capillary tube. If the length of capillary tube above the surface of water is made less than \(h\), then

(1). water rises upto a point a little below the top and stays there

(2). water does not rise at all.

(3). water rises upto the tip of capillary tube and then starts overflowing like a fountain

(4). water rises upto the top of capillary tube and stays there without overflowing

24. The value of coefficient of volume expansion of glycerin is \(5 × 10^4K^{−1}\).The fractional change in the density of glycerin for a rise of \(40^\circ C\) in its temperature, is

(1). \(0.025\)

(2). \(0.010\)

(3). \(0.015\)

(4). \(0.020\)

25. The Young’s modulus of steel is twice that of brass. Two wires of samelength and of same area of cross section, one of steel and another ofbrass are suspended from the same roof. If we want the lower ends ofthe wires to be at the same level, then the weights added to the steeland brass wires must be in the ratio of

(1). \(4 : 1\)

(2). \(1 : 1\)

(3). \(1 : 2\)

(4). \(2 : 1\)

26. The two ends of a metal rod are maintained at temperatures \(100^\circ C\) and \(110^\circ C\). The rate of heat flow in the rod is found to be \(4.0 J/s\). If the ends are maintained at temperatures \(200^\circ C\) and \(210^\circ C\), the rate of heat flow will be

(1). \(8.0 J/s\)

(2). \(4.0 J/s\)

(3). \(44.0 J/s \)

(4). \(16.8 J/s \)

27. A wind with speed \(40 m/s\) blows parallel to the roof of a house. The area of the roof is \(250 m^2\). Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be \(\left(\rho_{air} = 1.2kg/m^3\right)\)

(1). \(2.4 × 10^5 N\), upwards

(2). \(2.4 × 10^5 N\), downwards

(3). \(4.8 × 10^5 N\), downwards

(4). \(4.8 × 10^5 N\), upwards

28. The approximate depth of an ocean is \(2700 m\). The compressibility of water is \(45.4 × 10^{−11}Pa^{−1}\) and density of water is \(10^3 kg/m^3\). What fractional compression of water will be obtained at the bottom of the ocean?

(1). \(1.2 × 10^{−2}\)

(2). \(1.4 × 10^{−2}\)

(3). \(0.8 × 10^{−2}\)

(4). \(1.0 × 10^{−2}\)

29. On observing light from three different stars \(P\), \(Q\) and \(R\), it was found that intensity of violet colour is maximum in the spectrum of \(P\), the intensity of green colour is maximum in the spectrum of \(R\) and the intensity of red colour is maximum in the spectrum of \(Q\). If \(T_P\), \(T_Q\) and \(T_R\) are the respective absolute temperatures of \(P\), \(Q\) and \(R\), then it can be concluded from the above observations that

(1). \(T_P < T_R < T_Q \)

(2). \(T_P < T_Q < T_R\)

(3). \(T_P > T_Q > T_R\)

(4). \(T_P > T_R > T_Q\)

30. A particle is executing SHM along a straight line. Its velocities at distances \(x_1\) and \(x_2\) from the mean position are \(V_1\) and \(V_2\), respectively. Its time period is

(1). 2π \(\sqrt{\frac{V_1^2 + V_2^2}{x_1^2 + x_2^2}}\)

(2). 2π \(\sqrt{\frac{V_1^2 - V_2^2}{x_1^2 - x_2^2}}\)

(3). 2π \(\sqrt{\frac{x_1^2 + x_2^2}{V_1^2 + V_2^2}}\)

(4). 2π \(\sqrt{\frac{x_1^2 - x_2^2}{V_1^2 - V_2^2}}\)

31. A particle is executing a simple harmonic motion. Its maximum acceleration is a and maximum velocity is \(p\). Then, its time period of vibration will be

(1). \(\frac{β^2}{α}\)

(2). \(\frac{2πβ}{α}\)

(3). \(\frac{β^2}{α^2}\)

(4). \(\frac{α}{β}\)

32. A string is stretched between fixed points separated by \(75.0\,cm\). It is observed to have resonant frequencies of \(420\,Hz\) and \(315\,Hz\). There are no other resonant frequencies between these two. The lowest resonant frequency for this string is

(1). \(10.5\, Hz\)

(2). \(105\, Hz\)

(3). \(155\, Hz\)

(4). \(205\, Hz\)

33. \(4.0\, g\) of a gas occupies \(22.4\, litres\) at NTP. The specific heat capacity of the gas at constant volume is \(5.0\,J K^{−1}mol^{ −1}\). If the speed of sound in this gas at NTP is \(952\,ms^{−1}\), then the heat capacity at constant pressureis (Take gas constant \(R = 8.3\,J K^{−1}mol^{ −1}\))

(1). \(7.0\,J K^{ −1}mol^{ −1}\)

(2). \(8.5\,J K^{ −1}mol^{ −1}\)

(3). \(8.0\,J K^{ −1}mol^{ −1}\)

(4). \(7.5\,J K^{ −1}mol^{ −1}\)

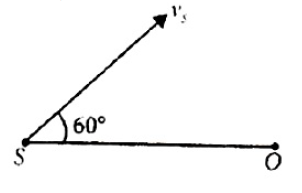
34. A source of sound \(S\) emitting waves of frequency \(100\,Hz\) and an observer \(O\) are located at some distance from each other. The source is moving with a speed of \(19.4\,ms^1\) at an angle of \(60^\circ\) with the source observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer (velocity of sound in air \(330\,ms^{−1}\)), is

(1). \(106\, Hz\)

(2). \(97\, Hz\)

(3). \(100\, Hz\)

(4). \(103\, Hz\)

35. The fundamental frequency of a closed organ pipe of length \(20\, cm\) is equal to the second overtone of an organ pipe open at both the ends.The length of organ pipe open at both the ends is

(1). \(120\, cm\)

(2). \(140\, cm\)

(3). \(80\, cm\)

(4). \(100\, cm\)

36. An electron moving in a circular orbit of radius r makes n rotations per second. The magnetic field produced at the centre has magnitude

(1). \(\displaystyle\frac{µ_0n^2e}{r}\)

(2). \(\displaystyle\frac{µ_0ne}{2r}\)

(3). \(\displaystyle\frac{µ_0ne}{2πr}\)

(4). \(Zero\)

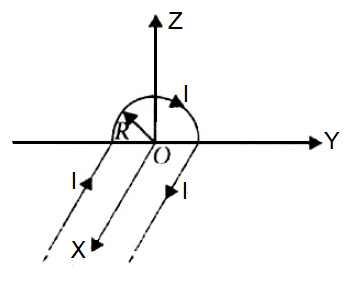
37. A wire carrying current I has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicircular portion of radius R is lying in Y-Z plane. Magnetic field at point O is

(1). \(\displaystyle\vec{B} = - \frac{µ_0 I}{4π R} \left(π\hat{i} + 2\hat{k}\right)\)

(2). \(\displaystyle\vec{B} = \frac{µ_0 I}{4π R} \left(π\hat{i} - 2\hat{k}\right)\)

(3). \(\displaystyle\vec{B} = \frac{µ_0 I}{4π R} \left(π\hat{i} + 2\hat{k}\right)\)

(4). \(\displaystyle\vec{B} = - \frac{µ_0 I}{4π R} \left(π\hat{i} - 2\hat{k}\right)\)

38. A proton and an alpha particle both enter a region of uniform magnetic field B, moving at right angles to the field B. If the radius of circular orbits for both the particles is equal and the kinetic energy acquired by proton is 1 MeV, the energy acquired by the alpha particle will be

(1). 1.5 MeV

(2). 1 MeV

(3). 4 MeV

(4). 0.5 MeV

39. A remote-sensing satellite of earth revolves in a circular orbit at a height of \(0.25 × 10^6\, m\) above the surface of earth. If earth’s radius is \(6.38 × 10^6\,m\) and \(g = 9.8\,ms^{−2}\), then the orbital speed of the satellite is

(1). \(9.13\,kms^{−1}\)

(2). \(6.67\,kms^{−1}\)

(3). \(7.76\,kms^{−1}\)

(4). \(8.56\,kms^{−1}\)

40. A satellite S is moving in an elliptical orbit around the earth. The massof the satellite is very small compared to the mass of the earth. Then,

(1). the linear momentum of 5 remains constant in magnitude.

(2). the acceleration of S is always directed towards the centre of the earth.

(3). the angular momentum of S about the centre of the earth changes in direction, but its magnitude remains constant

(4). the total mechanical energy of S varies periodically with time.

41. Kepler’s third law states that square of period of revolution (T) of aplanet around the sun, is proportional to third power of average distance r between sun and planet i.e.\(T^2 = K r^3\) here K is constant. If the masses of sun and planet are M and m respectively then as per Newton’s law of gravitation force of attraction between them is \(F = \frac{GMm}{r^2}\), here G is gravitational constant.The relation between G and K is described as

(1). \(K = G\)

(2). \(K = 1/G\)

(3). \(GK = 4π^2\)

(4). \(GM K = 4π^2\)

42. Two spherical bodies of mass M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12R.If they attract each other due to gravitational force only, then the distance covered by the smaller body before collision is

(1). 7.5 R

(2). 1.5 R

(3). 2.5 R

(4). 4.5 R

43. A resistance 'P' draws power 'P' when connected to an AC source. If an inductance is now placed in series with the resistance, such that the impedance of the circuit becomes 'Z' the power drawn will be

(1). \(P \left(\frac{R}{Z}\right)\)

(2). \(P\)

(3). \(P \left(\frac{R}{Z}\right)^2\)

(4). \(P \sqrt{\frac{R}{Z}}\)

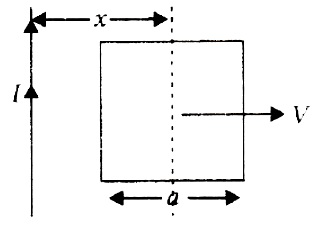
44. A conducting square frame of side ‘a ’ and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity ‘V’. The emf induced in the frame will be proportional to

(1). \(\frac{1}{\left(2x + a\right)^2}\)

(2). \(\frac{1}{\left(2x - a\right)\left(2x +a \right)}\)

(3). \(\frac{1}{x^2}\)

(4). \(\frac{1}{\left(2x - a\right)^2}\)

45. A series R-C circuit is connected to an alternating voltage source.Consider two situations(a) When capacitor is air filled.(b) When capacitor is mica filled. Current through resistor is i and voltage across capacitor is V then

(1). i_a > i_b

(2). V_a = V_b

(3). V_a < V_b

(4). V_a > V_b

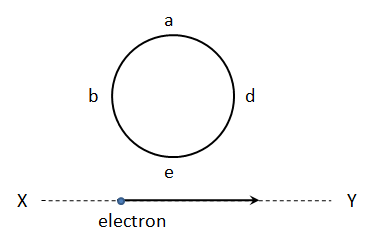
46. An electron moves on a straight line path X Y as shown. The abed is a coil adjacent to the path of electron. What will be the direction of current, if any, induced in the coil?

(1). The current will reverse its direction as the electron goes past the coil

(2). No current induced

(3). abed

(4). adcb

47. The electric field in a certain region is acting radially outward and is given by E = Ar. A charge contained in a sphere of radius 'a' centred at the origin of the field, will be given by

(1). \(4πε_0Aa^3\)

(2). \(ε_0Aa^3\)

(3). \(4πε_0Aa^2\)

(4). \(Aε_0a^2\)

48. A parallel plate air capacitor of capacitance C is connected to a cell ofemf V and then disconnected from it. A dielectric slab of dielectricconstant K, which can just fill the air gap of the capacitor, is nowinserted in it. Which of the following is incorrect?

(1). The change in energy stored is \(\frac{1}{2}CV^2\left(\frac{1}{k}-1\right)\)

(2). The charge on the capacitor is not conserved.

(3). The potential difference between the plates decreases K times.

(4). The energy stored in the capacitor decreases K. times.

49. A parallel plate air capacitor of capacitance C is connected to a cell ofemf V and then disconnected from it. A dielectric slab of dielectric constant K, which can just fill the air gap of the capacitor, is now inserted in it. Which of the following is incorrect ?

(1). The energy stored in the capacitor decreases K times.

(2). The change in energy stored is \(\frac{1}{2}CV^2\left(\frac{1}{k}-1\right)\)

(3). The charge on the capacitor is not conserved.

(4). The potential difference between the platesdecreases K times.

50. If potential (in volts) in a region is expressed as V (x, y, z) = 6xy - y + 2yz, the electric field (in N/C) at point (1, 1, 0) is

(1). \(-\left(2\hat{i}+3\hat{j}+\hat{k}\right)\)

(2). \(-\left(6\hat{i}+9\hat{j}+\hat{k}\right)\)

(3). \(-\left(3\hat{i}+5\hat{j}+3\hat{k}\right)\)

(4). \(-\left(6\hat{i}+5\hat{j}+2\hat{k}\right)\)

51. IF energy (E), velocity (v) and time (T) are chosen as the fundamental quantities, the dimensional formula of surface tension will be

(1). [ \(Ev^{-2}T^{-1}\) ]

(2). [ \(Ev^{-1}T^{-2}\) ]

(3). [ \(Ev^{-2}T^{-2}\) ]

(4). [ \(E^{-2}v^{-1}T^{-3}\) ]

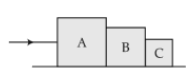
52. Three blocks A, B, and C of masses 4 kg, 2 kg and 1 kg respectively, are in contact on a frcitionless surface, as shown. If a force of 14 N is applied on the 4 kg block, then the contact force between A and B is

(1). 2 N

(2). 6 N

(3). 8 N

(4). 18 N

53. A block of mass 10 Kg, moving in x-direction with a constant speed of \(10\, \text{ms}^{-1}\), is subjected to a retarding force
F = 0.1 x J/m during its travel from x = 20 m to 30 m. Its final KE will be

(1). 475 J

(2). 450 J

(3). 275 J

(4). 250 J

54. Figure below shows two paths that may be taken by a gas to go from a state A to a state C.

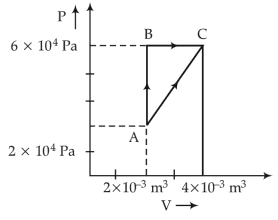
In process AB, 400 J of heat is added to the system and in process BC, 100 J of heat is added to the system. The heat absorbed by the system in the process AC will be

(1). 380 J

(2). 500 J

(3). 460 J

(4). 300 J

55. A carnot engine, having an efficiency of \(\displaystyle \eta\,=\,\frac{1}{10}\) as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservior at lower temperature is

(1). 100 J

(2). 99 J

(3). 90 J

(4). 1 J

56. One mole of an ideal diatomic gas undergoes a transition from A to B a transition from A to B along a path AB as shown in the figure,

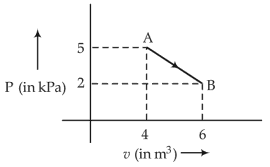
The change in internal energy of the gas during the transition is:

(1). 20kJ

(2). -20kJ

(3). 20J

(4). -12kJ

57. When two displacements represented by \(y_1\,=\, a\, sin\, \left(\omega\,t\right)\) and \(y_2\,=\, b\, cos\, \left(\omega\,t\right)\)are superimposed the motion is:

(1). not a simple harmonic

(2). simple harmonic with amplitude \(\displaystyle \frac{a}{b}\)

(3). simple harmonic with amplitude \(\displaystyle \sqrt{a^2\,+\,b^2}\)

(4). simple harmonic with amplitude \(\displaystyle \frac{\left(a\,+\,b\right)}{2}\)

58. A radiation of energy ‘E’ falls normally on a perfectly reflecting surface The momentum transferred to the surface is (C = Velocity of light):

(1). \(\displaystyle \frac{E}{C}\)

(2). \(\displaystyle \frac{2E}{C}\)

(3). \(\displaystyle \frac{2E}{C^2}\)

(4). \(\displaystyle \frac{E}{C^2}\)

59. Two identical thin plano – convex glass lenses (refractive index 1.5) each having radius of curvature of 20 cm are placed with their convex surface in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is:

(1). - 20 cm

(2). - 20 cm

(3). - 50 cm

(4). 50 cm

60. For a parallel beam of monochromatic light of wavelength ‘λ’, diffraction is produced by a single slit whose width ‘a’ is of the order of the wavelength of the light. If ‘D’ is the distance of the screen from the slit, the width of the central maxima will be:

(1). \(\displaystyle \frac{2D\lambda}{a}\)

(2). \(\displaystyle \frac{D\lambda}{a}\)

(3). \(\displaystyle \frac{Da}{\lambda}\)

(4). \(\displaystyle \frac{2Da}{\lambda}\)

61. In a double slit experiment, the two slits are 1 mm apart and the screen is placed 1 m away. A monochromatic light of wavelength 500 nm is used. What will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single slit pattern?

(1). 0.2 mm

(2). 0.1 mm

(3). 0.5 mm

(4). 0.02 mm

62. The refracting angle of a prism is A, and refractive index of the material of the prism is cot(A/2). The angle of minimum deviation is:

(1). 180° - 3A

(2). 180° - 2A

(3). 90° - A

(4). 180° 2A

63. A certain metallic surface is illuminated with monochromatic light of wavelength, \(\lambda\). The stopping potential for photo-electric current for this light is \(3V_0\). If the same surface is illuminated with light of wavelength \(2\,\lambda\), the stopping potential is \(V_0\). The threshold wavelength for this surface for photo-electric effect is:

(1). \(6\,\lambda\)

(2). \(4\,\lambda\)

(3). \(\displaystyle \frac{\lambda}{4}\)

(4). \(\displaystyle \frac{\lambda}{6}\)

64. Consider \(3^{rd}\) orbit of \(\text{He}^+\) (Helium), using non-relativistic approach, the speed of electron in this orbit will be (given \(\text{K}\, =\,9 \times 10^9\) constant, \(\text{Z}\,=\,2\) and \(\text{h (Planck's constant)}\,=\,6.6 \times 10^{-34}Js\)

(1). \(2.92 \times 10^6\,m/s\)

(2). \(1.46 \times 10^6\,m/s\)

(3). \(0.73 \times 10^6\,m/s\)

(4). \(3.0 \times 10^8\,m/s\)

65. If radius of the \(_{13}\text{Al}^{27}\) nucleus is taken to be \(R_{\text{Al}}\), then the radius of \(_{53}\text{Te}^{125}\) nucleus is nearly

(1). \(\displaystyle \left(\frac{53}{13} \right)^{\frac{1}{3}} R_{Al}\)

(2). \(\displaystyle \frac{5}{3}R_{\text{Al}}\)

(3). \(\displaystyle \frac{3}{5}R_{\text{Al}}\)

(4). \(\displaystyle \frac{13}{53}R_{\text{Al}}\)

66. The ratio of specific heats \(\displaystyle \frac{C_p}{C_v}\,=\, \gamma\) in terms of degrees of freedom (n) is given by:

(1). \(\displaystyle \left(1\,+\,\frac{1}{n} \right)\)

(2). \(\displaystyle \left(1\,+\,\frac{n}{3} \right)\)

(3). \(\displaystyle \left(1\,+\,\frac{2}{n} \right)\)

(4). \(\displaystyle \left(1\,+\,\frac{n}{2} \right)\)

Limited-Time Offer: Get all this for just ₹1199

Why settle for outdated methods when you can prepare smarter, track better, and score higher? Subscribe Now & Take Control of Your NEET Prep !

Your Full Test Performance Summary

Why settle for outdated methods when you can prepare smarter, track better, and score higher?
Subscribe Now & Take Control of Your NEET Prep !