Your Performance Summary!
Questions Available: 25
Questions Attempted: 0
Number of Attempts: 0
Correct Attempts: 0
Total Time Spent: 00:00
Avg Time Per Question: 00:00
Solution
Year: 2024
Topic: Oscillations
2. The two-dimensional motion of a particle, described by \(\vec{r}\) = \(\left(\hat{i} + 2\hat{j}\right) A cos ωt\) is a/an:
A. parabolic path
B. elliptical path
C.periodic motion
D. simple harmonic motion.
Choose the correct answer from the options given below:
A. parabolic path
B. elliptical path
C.periodic motion
D. simple harmonic motion.
Choose the correct answer from the options given below:
(1).B, C and D only
(2). A, B and C only
(3). A, C and D only
(4). C and D only
Solution
Solution
Year: 2024
Topic: Oscillations
4. If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then thenew time period of oscillation is \(x/2\) times its original time period. Then the value of x is:
(1).\(\sqrt{3}\)
(2). \(\sqrt{2}\)
(3). \(2 \sqrt{3}\)
(4). \(4\)
Solution
Year: 2023
Topic: Oscillations
5. The x-t graph of a particle performing simple harmonic motion is shown in the figure. The acceleration of the particle at \(t = 2s\) is
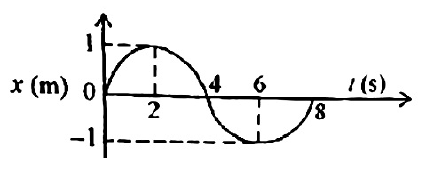

(1).\(- \frac{π^2}{8} ms^{-2}\)
(2). \(\frac{π^2}{16}ms^{-2}\)
(3). \(- \frac{π^2}{16} ms^{-2}\)
(4). \(\frac{π^2}{8} ms^{-2}\)
Solution
Year: 2023
Topic: Oscillations
6. A simple pendulum oscillating in air has a period of \(\sqrt{3}s\). If it is completely immersed in non-viscous liquid, having density \(\left(1/4\right)^{th}\) of the material of the bob, the new period will be :-
(1).\(2\sqrt{3}s\)
(2). \(\frac{2}{\sqrt{3}}s\)
(3). \(2 s\)
(4). \(\frac{\sqrt{3}}{2}s\)
Solution
Year: 2022
Topic: Oscillations
7. Two pendulums of length \(121 cm\) and \(100 cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is:
(1).\(11\)
(2). \(9\)
(3). \(10\)
(4). \(8\)
Solution
Solution
Solution
Solution
Solution
Year: 2019
Topic: Oscillations
12. The displacement of a particle executing simple harmonic motion isgiven by \(y = A_0 + A sin ω t + B cos ω t\). Then the amplitude of its oscillation is given by
(1).\(A + B\)
(2). \( A_0 + \sqrt{A^2 + B^2}\)
(3). \(\sqrt{A^2 + B^2}\)
(4). \(\sqrt{{A_0}^2 + \left(A + B\right)^2}\)
Solution
Solution
Year: 2019
Topic: Oscillations
14. The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.
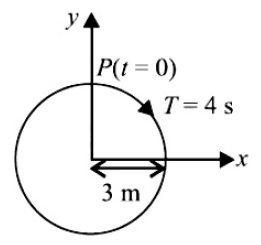
y - projection of the radius vector of rotating particle \(P\) is

y - projection of the radius vector of rotating particle \(P\) is
(1).\(y(t) = 3 cos \left(\frac{πt}{2}\right)\), where y in m
(2). \(y(t) = −3 cos 2 π t\), where y in m
(3). \(y(t) = 4 sin \left(\frac{πt}{2}\right)\), where y in m
(4). \(y(t) = 3 cos \left(\frac{3πt}{2}\right) \), where y in m
Solution
Solution
Year: 2018
Topic: Oscillations
16. A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is \(20ms^{−2}\) at a distance of 5mfrom the mean position. The time period of oscillation is
(1).\(2πs\)
(2). \(πs\)
(3). \(2s\)
(4). \(1s\)
Solution
Year: 2017
Topic: Oscillations
17. A spring of force constant k is cut into lengths of ratio \(1 : 2 : 3\). They are connected in series and the new force constant is \(k'\).Then they are connected in parallel and force constant is \(k''\).Then \(k' : k''\) is
(1).\(1 : 9\)
(2). \(1 : 11\)
(3). \(1 : 14\)
(4). \(1 : 6\)
Solution
Year: 2017
Topic: Oscillations
18. A particle executes linear simple harmonic motion with an amplitude of \(3\, cm\). When the particle is at \(2\, cm\) from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is
(1).\(\frac{\sqrt{5}}{2π}\)
(2). \(\frac{4π}{\sqrt{5}}\)
(3). \(\frac{2π}{\sqrt{3}}\)
(4). \(\frac{\sqrt{5}}{π}\)
Solution
Year: 2016
Topic: Oscillations
19. A body of mass m is attached to the lower end of a spring whose upperend is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of \(3\, s\). When the mass m is increased by \(1\, kg\), the time period of oscillationsbecomes \(5\, s\). The value of \(m\) in kg is
(1).\(\frac{3}{4}\)
(2). \(\frac{4}{3}\)
(3). \(\frac{16}{9}\)
(4). \(\frac{9}{16}\)
Solution
Year: 2015
Topic: Oscillations
20. A particle is executing SHM along a straight line. Its velocities at distances \(x_1\) and \(x_2\) from the mean position are \(V_1\) and \(V_2\), respectively. Its time period is
(1).2π \(\sqrt{\frac{V_1^2 + V_2^2}{x_1^2 + x_2^2}}\)
(2). 2π \(\sqrt{\frac{V_1^2 - V_2^2}{x_1^2 - x_2^2}}\)
(3). 2π \(\sqrt{\frac{x_1^2 + x_2^2}{V_1^2 + V_2^2}}\)
(4). 2π \(\sqrt{\frac{x_1^2 - x_2^2}{V_1^2 - V_2^2}}\)
Solution
Solution
Year: 2014
Topic: Oscillations
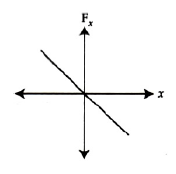
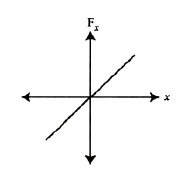
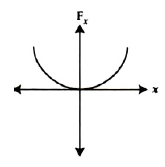
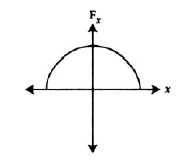
22. The oscillation of a body on a smooth horizontal surface is represented by the equation, \(X = A cos(ωt)\) Where \(X\) = displacement at time \(t\), \(ω\) = frequency of oscillation. Which one of the following graphs shows correctly the variation a with \(t\) ? Here \(a\) = acceleration at time \(T\) = time period
(1).
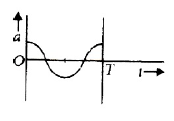
(2).
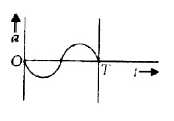
(3).
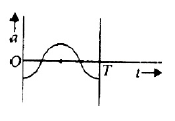
(4).
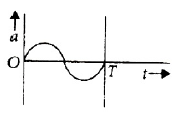
Solution
Solution
Year: 2025
Topic: Oscillations
24. In an oscillating spring mass system, a spring is connected to a box filled with sand. As the box oscillates, sand leaks slowly out of the box vertically so that the average frequency \(\omega\left(\text{t}\right)\) and average amplitude \(\text{A}\left(\text{t}\right)\) of the system change with time t. Which one of the following options schematically depicts these changes correctly?
(1).
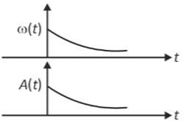
(2).
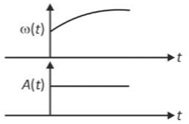
(3).
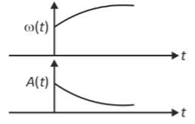
(4).

Solution
Year: 2025
Topic: Oscillations
25. Two identical point masses P and Q, suspended from two separate massless springs of spring constants \(\text{k}_1\) and \(\text{k}_2\), respectively, oscillate vertically. if their maximum speeds are the same, the ratio (\( \text{A}_Q\)/\(\text{A}_P\)) of the amplitude \(\text{A}_Q\) of mass Q to the amplitude \(\text{A}_P\) of mass P is
(1).\(\displaystyle \sqrt{\frac{\text{K}_1}{\text{K}_2}}\)
(2). \(\displaystyle \frac{\text{K}_2}{\text{K}_1}\)
(3). \(\displaystyle \frac{\text{K}_1}{\text{K}_2}\)
(4). \(\displaystyle \sqrt{\frac{\text{K}_2}{\text{K}_1}}\)