1. An ideal fluid is flowing in a non-uniform cross-sectional tube X Y (as shown in the figure) from end X to end Y. If K₁ and K₂ are the kinetic energy per unit volume of the fluid at X and Y respectively, then the correct option is:

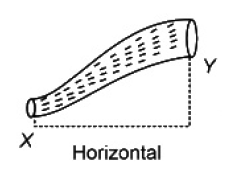
(1).K₁ = K₂

(2). 2K₁ = K₂

(3). K₁ > K₂

(4). K₁ < K₂

2. The maximum elongation of a steel wire of 1m length if the elastic limit of steel and its Young's modulus, respectively, are 8 × 10⁸Nm⁻² and 2 ×10¹¹Nm⁻², is:

(1).4 mm

(2). 0.4 mm

(3). 40 mm

(4). 8 mm

3. A thin flat circular disc of radius 4.5 cm is placed gently over the surface of water. If surface tension of water is 0.07Nm⁻¹, then the excess force required to take it away from the surface is

(1).19.8 mN

(2). 198 N

(3). 1.98 mN

(4). 99 N

4. A metallic bar of Young's modulus, \(0.5 × 10^{11}Nm^{−2}\) and coefficient of linear thermal expansion \(10^{−5^\circ}C^{−1}\), length 1m and area of cross section \(10^{−3}m^2\) is heated from \(0^\circ C\) to \(100^\circ C\) with out expansion or bending. The compressive force developed in it is:

(1). 5 × 10³ N

(2). 50 × 10³ N

(3). 100 × 10³ N

(4). 2 × 10³ N

5. Let a wire be suspended from the ceiling (rigid support) and stretchedby a weight W attached at its free end. The longitudinal stress at anypoint of cross-sectional area A of the wire is

(1).\(\frac{W}{A}\)

(2). \(\frac{W}{2A}\)

(3). Zero

(4). \(\frac{2W}{A}\)

6. The amount of energy required to form a soap bubble of radius 2cm from a soap solution is nearly (surface tension of soap solution = 0.03Nm⁻¹)

(1).\(5.06 × 10^{−4}J\)

(2). \(3.01 × 10^{−4}J\)

(3). \(50.1 × 10^{−4}J\)

(4). \(30.16 × 10^{−4}J\)

7. The venturi-meter works on

(1).Bernoulli's principle

(2). The principle of parallel axes

(3). The principle of perpendicular axes

(4). Huygens's principle

8. The amount of elastic potential energy per unit volume (in SI unit) of a steel wire of length 100 cm to stretch it by 1mm is (if Young's modulusof the wire = 2.0 × 10¹¹Nm⁻²) :

(1).\(10^{11}\)

(2). \(10^{17}\)

(3). \(10^7\)

(4). \(10^5\)

9. Which of the following statement is not true?

(1).Coefficient of viscosity is a scalar quantity

(2). Surface tension is a scalar quantity

(3). Pressure is a vector quantity

(4). Relative density is a scalar quantity

10. The viscous drag acting on a metal sphere of diameter 1 mm, falling through a fluid of viscosity 0.8 Pa s with a velocity of 2m s⁻¹ is equal to :

(1).\(15×10^{−3}N\)

(2). \(30×10^{−3}N\)

(3). \(1.5×10^{−3}N\)

(4). \(20×10^{−3}N\)

11. A spherical ball is dropped in a long column of a highly viscous liquid.The curve in the graph shown, which represents the speed of the ball (v) as a function of time (t) is

(1).A

(2). B

(3). C

(4). D

12. If a soap bubble expands, the pressure inside the bubble

(1).Decreases

(2). Increases

(3). Remains the same

(4). Is equal to the atmospheric pressure

13. Given below are two statements : One is labelled as Assertion (A) and the other is labelled as Reason (R). Assertion (A): The stretching of a spring is determined by the shear modulus of the material of the spring.
Reason (R): A coil spring of copper has more tensile strength than asteel spring of same dimensions.
In the light of the above statements, choose the most appropriateanswer from the options given below

(1).Both (A) and (R) are true and (R) is the correct explanation of (A)

(2). Both (A) and (R) are true and (R) is not the correct explanation of (A)

(3). (A) is true but (R) is false

(4). (A) is false but R ) is true

14. Two copper vessels A and B have the same base area but of differentshapes. A take twice the volume of water as that B requires to fill upto aparticular common height. Then the correct statement among thefollowing is:

(1).Vessel B weighs twice that of A.

(2). Pressure on the base area of vessels A and B is same.

(3). Pressure on the base area of A and B is not same.

(4). Both vessels A and B weigh the same.

15. A The terminal velocity of a copper ball of radius 5mm falling through a tank of oil at room temperature is 10cms⁻¹. If the viscosity of oil at room temperature is 0.9kgm⁻¹ s⁻¹, the viscous drag force is:

(1).\(4.23 × 10^{−6}N\)

(2). \(8.48 × 10^{−3}N\)

(3). \(8.48 × 10^{−5}N\)

(4). \(4.23 × 10^{−3}N\)

16. Two rods one made of copper and other made of steel of the samelength and same cross sectional area are joined together. The thermal conductivity of copper and steel are 385Js⁻¹K⁻¹m⁻¹ and 50Js⁻¹K⁻¹m⁻¹ respectively. The free ends of copper and steel are held at \(100^\circ C\) and \(0^\circ C\) respectively. The temperature at the junction is, nearly:

(1).\(88.5^\circ C\)

(2). \(12^\circ C\)

(3). \(50^\circ C\)

(4). \(73^\circ C\)

17. The velocity of a small ball of mass M and density d , when dropped in acontainer filled with glycerine becomes constant after some time. If thedensity of glycerine is \(\frac{d}{2}\), then the viscous force acting on the ball will be

(1).\(\frac{Mg}{2}\)

(2). \(Mg\)

(3). \(\frac{3}{2}Mg\)

(4). \(2Mg\)

18. A wire of length L, area of cross section A is hanging from a fixed support. The length of the wire changes to L₁ when mass M is suspended from its free end. The expression for Young's modulus is :

(1).\(\frac{M g\left(L_1 - L\right)}{AL}\)

(2). \(\frac{MgL}{AL_1}\)

(3). \(\frac{M gL}{A\left(L_1 - L\right)}\)

(4). \(\frac{MgL_1}{AL}\)

19. A capillary tube of radius r is immersed in water and water rises in it to a height h. The mass of the water in the capillary is 5g. Another capillary tube of radius 2r is immersed in water. The mass of water that will rise in this tube is :

(1).5.0 g

(2). 10.0 g

(3). 20.0 g

(4). 2.5 g

20. A copper rod of 88cm and an aluminium rod of unknown length have their increase in length independent of increase in temperature. The length of aluminium rod is \(\left(\alpha_{Cu} = 1.7 × 10^{−5}K^{−1}, \alpha_{Al} = 2.2 × 10^{−5}K^{−1}\right)\)

(1).68 cm

(2). 6.8 cm

(3). 113.9 cm

(4). 88 cm

21. A small hole of area of cross-section \(2 mm^2\) is present near the bottom ofa fully filled open tank of height \(2 m\). Taking \(g = 10 m ∕ s^2\), the rate offlow of water through the open hole would be nearly

(1).\(6.4 × 10^{−6}m^3 ∕ s\)

(2). \(12.6 × 10^{−6}m^3 ∕ s\)

(3). \(8.9 × 10^{−6}m^3 ∕ s\)

(4). \(2.23 × 10^{−6}m^3 ∕ s\)

22. When a block of mass M is suspended by a long wire of length L, thelength of the wire becomes (L + l ). The elastic potential energy storedin the extended wire is

(1).\(\frac{1}{2}\) MgL

(2). Mgl

(3). MgL

(4). \(\frac{1}{2}\) Mgl

23. A soap bubble, having radius of 1mm, is blown from a detergentsolution having a surface tension of \(2.5 × 10^{−2}N ∕ m\). The pressure inside the bubble equals at a point \(Z_0\) below the free surface of water in a container. Taking \(g = 10 m ∕ s^2\), density of water = \(10^3kg ∕ m^3\), the value of \(Z_0\) is

(1).0.5 cm

(2). 100 cm

(3). 10 cm

(4). 1 cm

24. Two small spherical metal balls, having equal masses, are made from materials of densities \(\rho_1\) and \(\rho_2 \left(\rho_1 = 8\rho_2\right)\) and have radii of 1mm and2mm, respectively. They are made to fall vertically (from rest) in aviscous medium whose coefficient of viscosity equals \(\eta\) and whose density is \(0.1\rho_2\). The ratio of their terminal velocities would be

(1).\(\frac{79}{72}\)

(2). \(\frac{19}{36}\)

(3). \(\frac{39}{72}\)

(4). \(\frac{79}{36}\)

25. The stress-strain curves are drawn for two different materials X and Y .It is observed that the ultimate strength point and the fracture point areclose to each other for material X but are far apart for material Y . Wecan say that materials X and Y are likely to be (respectively)

(1).ductile and brittle

(2). brittle and ductile

(3). brittle and plastic

(4). plastic and ductile

26. A small sphere of radius \('r'\) falls from rest in a viscous liquid. As a result, heat is produced due to viscous force. The rate of production ofheat when the sphere attains its terminal velocity, is proportional to

(1).\(r^3\)

(2). \(r^2\)

(3). \(r^5\)

(4). \(r^4\)

27. Two wires are made of the same material and have the same volume.The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by \(\Delta l \) on applying a force \(F\) , how much force is needed to stretch the second wire by the same amount?

(1).\(9 F \)

(2). \(6 F \)

(3). \(4 F\)

(4). \(F\)

28. The power radiated by a black body is \(P\) and it radiates maximum energy at wavelength, \(\lambda_0\). If the temperature of the black body is now changed so that it radiates maximum energy at wavelength \(\frac{3}{4} \lambda_0\), the power radiated by it becomes \(n_p\). The value of n is

(1).\(\frac{3}{4}\)

(2). \(\frac{4}{3}\)

(3). \(\frac{256}{81}\)

(4). \(\frac{81}{256}\)

29. Two rods \(A\) and \(B\) of different materials are welded together as shown infigure. Their thermal conductivities are \(K_1\) and \(K_2\) The thermal conductivity of the composite rod will be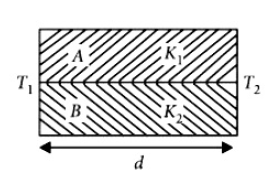

(1).\(\frac{3\left(K_1 + K_2\right)}{2}\)

(2). \(K_1 + K_2\)

(3). \(2\left(K_1 + K_2\right)\)

(4). \(\frac{K_1 + K_2}{2}\)

30. A spherical black body with a radius of \(12 cm\) radiates \(450 watt\) power at \(500 K\). If the radius were halved and the temperature doubled, thepower radiated in watt would be

(1).\(450\)

(2). \(1000\)

(3). \(1800\)

(4). \(225\)

31. A U tube with both ends open to the atmosphere, is partially filled with water. Oil, which is immiscible with water, is poured into one side untilit stands at a distance of \(10 mm\) above the water level on the other side. Meanwhile the water rises by \(65 mm\) from its original level (see diagram). The density of the oil is

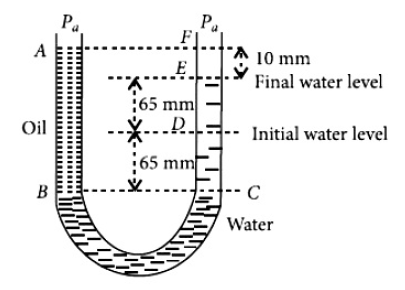
(1).\(425 kgm^{-3}\)

(2). \(800 kgm^{−3}\)

(3). \(928 kgm^{−3}\)

(4). \(650 kgm^{−3}\)

32. The bulk modulus of a spherical object is \('B'\). If it is subjected touniform pressure \('p'\) the fractional decrease in radius is

(1).\(\frac{B}{3p}\)

(2). \(\frac{3p}{B}\)

(3). \(\frac{p}{3B}\)

(4). \(\frac{P}{B}\)

33. Coefficient of linear expansion of brass and steel rods are \(\alpha_1\) and \(\alpha_2\). Length of brass and steel rods are \(l_1\) and \(l_2\) respectively. If \(\left(l_2 − l_1\right)\) is maintained same at all temperatures, which one of the following relations holds good?

(1).\({\alpha_1}^2 l_2 = {\alpha_2}^2l_1\)

(2). \(\alpha_1 l_1 = \alpha_2 l_ 2\)

(3). \(\alpha_1 l_ 2 = \alpha_2 l_1\)

(4). \(\alpha_1 l_ 2^2 = \alpha_2 l_1^2\)

34. A piece of ice falls from a height h so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of \(h\) is [Latent heat of ice is \(3.4 × 10^5 J/kg\) and \(g = 10 N/kg\)

(1).\(136 km\)

(2). \(68 km\)

(3). \(34 km\)

(4). \(544 km\)

35. A black body is at a temperature of \(5760 K\). The energy of radiation emitted by the body at wavelength \(250 nm\) is \(U_1\),at wavelength \(500 nm\) is \(U_2\) and that at \(1000 nm\) is \(U_3\) Wien's constant, \(b = 2.88 × 10^6nmK\) . Which of the following is correct?

(1).\(U_1 > U_2\)

(2). \(U_2 > U_1 \)

(3). \(U_1 = 0\)

(4). \(U_3 = 0\)

36. Two non-mixing liquids of densities \(p\) and \(np \left(n > 1\right)\) are put in a container. The height of each liquid is \(A\). A solid cylinder of length \(L\) and density \(d\) is put in this container. The cylinder floats with its axis vertical and length \(pL \left(p < 1\right)\) in the denser liquid. The density \(d\) is equal to

(1).\(\{2 + \left(n − 1\right)p\}\rho\)

(2). \(\{1 + \left(n − 1\right)p\}\rho\)

(3). \(\{1 + \left(n + 1\right)p\}\rho\)

(4). \(\{2 + \left(n + 1\right)p\}\rho\)

37. A rectangular film of liquid is extended from \(\left(4 cm × 2 cm\right)\) to \(\left(5 cm × 4 cm\right)\). If the work done is \(3 × 10^{−4}J\), the value of the surface tension of the liquid is

(1).\(0.250N m ^{−1}\)

(2). \(0.125N m ^{−1}\)

(3). \(0.2N m ^{−1}\)

(4). \(8.0N m ^{−1}\)

38. Three liquids of densities \(\rho_1\), \(\rho_2\) and \(\rho_3\) (with \(\rho_1 > \rho_2 > \rho_3\)),having the same value of surface tension \(T\), rise to the same height in three identical capillaries. The angles of contact \(θ_1\),\( θ_2\) and \(θ_3\) obey

(1).\(\frac{π}{2} > θ_1 > θ_2 > θ_3 ≥ 0\)

(2). \(0 ≤ θ_1 < θ_2 < θ_3 < \frac{π}{2}\)

(3). \(\frac{π}{2}< θ_1 < θ_2 < θ_3 < π\)

(4). \(π > θ_1 > θ_2 > θ_3 >\frac{π}{2}\)

39. Two identical bodies are made of a material for which the heat capacityincreases with temperature. One of these is at \(100^\circ C\), while the other one is at \(0^\circ C\). If the two bodies are brought into contact, then,assuming no heat loss, the final common temperature is

(1).\( 50^\circ C\)

(2). More than \( 50^\circ C\)

(3). less than \( 50^\circ C\) but greater than \( 0^\circ C\)

(4). \( 0^\circ C\)

40. A body cools from a temperature \(3T\) to \(2T\) in \(10\) minutes. The room temperature is \(T\). Assume that Newton’s law of cooling is applicable.The temperature of the body at the end of next \(10\) minutes will be

(1).\(\frac{7}{4}T\)

(2). \(\frac{3}{2}T\)

(3). \(\frac{4}{3}T\)

(4). \(T\)

41. The cylindrical tube of a spray pump has radius \(R\), one end of which has n fine holes, each of radius \(r\). If the speed of the liquid in the tube is \(V\),the speed of the ejection of the liquid through the holes is

(1).\(\frac{VR^2}{n^3r^2}\)

(2). \(\frac{V^2R}{nr}\)

(3). \(\frac{VR^2}{n^2r^2}\)

(4). \(\frac{VR^2}{nr^2}\)

42. Water rises to a height \(h\) in capillary tube. If the length of capillary tube above the surface of water is made less than \(h\), then

(1).water rises upto a point a little below the top and stays there

(2). water does not rise at all.

(3). water rises upto the tip of capillary tube and then starts overflowing like a fountain

(4). water rises upto the top of capillary tube and stays there without overflowing

43. The value of coefficient of volume expansion of glycerin is \(5 × 10^4K^{−1}\).The fractional change in the density of glycerin for a rise of \(40^\circ C\) in its temperature, is

(1).\(0.025\)

(2). \(0.010\)

(3). \(0.015\)

(4). \(0.020\)

44. The Young’s modulus of steel is twice that of brass. Two wires of samelength and of same area of cross section, one of steel and another ofbrass are suspended from the same roof. If we want the lower ends ofthe wires to be at the same level, then the weights added to the steeland brass wires must be in the ratio of

(1).\(4 : 1\)

(2). \(1 : 1\)

(3). \(1 : 2\)

(4). \(2 : 1\)

45. The two ends of a metal rod are maintained at temperatures \(100^\circ C\) and \(110^\circ C\). The rate of heat flow in the rod is found to be \(4.0 J/s\). If the ends are maintained at temperatures \(200^\circ C\) and \(210^\circ C\), the rate of heat flow will be

(1).\(8.0 J/s\)

(2). \(4.0 J/s\)

(3). \(44.0 J/s \)

(4). \(16.8 J/s \)

46. A wind with speed \(40 m/s\) blows parallel to the roof of a house. The area of the roof is \(250 m^2\). Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be \(\left(\rho_{air} = 1.2kg/m^3\right)\)

(1).\(2.4 × 10^5 N\), upwards

(2). \(2.4 × 10^5 N\), downwards

(3). \(4.8 × 10^5 N\), downwards

(4). \(4.8 × 10^5 N\), upwards

47. The approximate depth of an ocean is \(2700 m\). The compressibility of water is \(45.4 × 10^{−11}Pa^{−1}\) and density of water is \(10^3 kg/m^3\). What fractional compression of water will be obtained at the bottom of the ocean?

(1).\(1.2 × 10^{−2}\)

(2). \(1.4 × 10^{−2}\)

(3). \(0.8 × 10^{−2}\)

(4). \(1.0 × 10^{−2}\)

48. On observing light from three different stars \(P\), \(Q\) and \(R\), it was found that intensity of violet colour is maximum in the spectrum of \(P\), the intensity of green colour is maximum in the spectrum of \(R\) and the intensity of red colour is maximum in the spectrum of \(Q\). If \(T_P\), \(T_Q\) and \(T_R\) are the respective absolute temperatures of \(P\), \(Q\) and \(R\), then it can be concluded from the above observations that

(1).\(T_P < T_R < T_Q \)

(2). \(T_P < T_Q < T_R\)

(3). \(T_P > T_Q > T_R\)

(4). \(T_P > T_R > T_Q\)

49. Copper of fixed volume \(V\) is drawn into wire of length \(l\). When this wire is subjected to a constant force \(F\), the extension produced in the wire is \(\Delta l\). Which of the following graphs is a straight line?

(1).\(\Delta l\) versus \(1/l\)

(2). \(\Delta l\) versus \(l^2\)

(3). \(\Delta l\) versus \(\frac{1}{l^2}\)

(4). \(\Delta l\) versus \(l\)

50. A certain number of spherical drops of a liquid of radius \(r\) coalesce to form a single drop of radius \(R\) and volume \(V\) If \(T\) is the surface tension of the liquid, then

(1).energy = \(4V T \left(\frac{1}{r} - \frac{1}{R}\right)\) is released

(2). energy = \(3V T \left(\frac{1}{r} + \frac{1}{R}\right)\) is absorbed

(3). energy = \(3V T \left(\frac{1}{r} - \frac{1}{R}\right)\) is released

(4). energy is neither released nor absorbed

51. Steam at \(100^\circ C\) is passed into \(20 g\) of water at \(10^\circ C\). When water acquires a temperature of \(80^\circ C\), the mass of water present will be [Take specific heat of water = \(1cal g^{−1 \circ} C^{−1}\) and latent heat of steam = \(540 cal g^{−1}\)]

(1).\(24 g \)

(2). \(31.5 g \)

(3). \(42.5 g \)

(4). \(22.5 g \)

52. Certain quantity of water cools from \(70^\circ C\) to \(60^\circ C\) in the first \(5\) minutes and to \(54^\circ C\) in the next \(5\) minutes. The temperature of the surroundings is

(1).\(45^\circ C\)

(2). \(20^\circ C\)

(3). \(42^\circ C\)

(4). \(10^\circ C\)

53. Three identical heat conducting rods are connected in series as shown in the figure. The rods on the sides have thermal conductivity 2K while that in the middle has thermal conductivity K. The left end of the combination is maintained at temperature 3T and the right end at T. The rods are thermally insulated from outside. In steady state, temperature at the left junction is \(\text{T}_1\), and that at the right junction is \(\text{T}_2\). The ratio \(\text{T}_1\,\\,\text{T}_2\) is

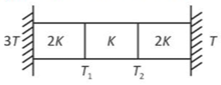
(1).\(\displaystyle \frac{5}{4}\)

(2). \(\displaystyle \frac{3}{2}\)

(3). \(\displaystyle \frac{4}{3}\)

(4). \(\displaystyle \frac{5}{3}\)