1. An object moving along horizontal x-direction with kinetic energy 10J is displaced through x = \(\left(3\hat{i}\right)\)m by the force \(\vec{F} = \left(-2\hat{i} + 3\hat{j}\right)\). The kinetic energy of the object at the end of the displacement x is

(1).10 J

(2). 16 J

(3). 4 J

(4). 6 J

2. An object falls from a height of 10m above the ground. After strikingthe ground it loses 50% of its kinetic energy. The height upto which theobject can rebounce from the ground is:

(1).7.5 m

(2). 10 m

(3). 2.5 m

(4). 5 m

3. The potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8 cm, potential energy stored in it will be

(1).4 U

(2). 8 U

(3). 16 U

(4). 2 U

4. At any instant of time t, the displacement of any particle is given by 2t −1 (SI unit) under the influence of force of 5N. The value of instantaneous power is (in SI unit):

(1).10

(2). 5

(3). 7

(4). 6

5. A bullet of mass m hits a block of mass M elastically.The transfer of energy is the maximum, when :

(1).M = m

(2). M = 2m

(3). M < < m

(4). M > > m

6. A particle moves with a velocity horizontally under the actionof constant force The instantaneous power supplied to theparticle is :

(1).200 W

(2). Zero

(3). 100 W

(4). 140 W

7. An electric lift with a maximum load of 2000kg (lift + passengers) ismoving up with a constant speed of 1.5ms⁻¹. The frictional force opposing the motion is 3000N . The minimum power delivered by the motor to the lift in watts is : (g = 10ms⁻²)

(1).23000

(2). 20000

(3). 34500

(4). 23500

8. The energy that will be ideally radiated by a 100kW transmitter in 1hour is

(1).36 × 10⁷ J

(2). 36 × 10⁴ J

(3). 36 × 10⁵ J

(4). 1 × 10⁵ J

9. The distance covered by a body of mass 5g having linear momentum0.3 kg m ∕ s in 5s is:

(1).0.3 m

(2). 300 m

(3). 30 m

(4). 3 m

10. Water falls from a height of 60 m at the rate of 15 kg/s to operate aturbine. The losses due to frictional force are 10% of the input energy.How much power is generated by the turbine?(g = 10 m/s2 )

(1).10.2 kW

(2). 8.1 kW

(3). 12.3 kW

(4). 7.0 kW

11. Body A of mass 4m moving with speed u collides with another body B ofmass 2m, at rest. The collision is head on and elastic in nature. After the collision the fraction of energy lost by the colliding body A is

(1).5 / 9

(2). 1 / 9

(3). 8 / 9

(4). 4 / 9

12. A force F = 20 + 10y acts on a particle in y -direction where F is in newton and y in meter. Work done by this force to move the particle from y = 0 to y = 1m is

(1).20 J

(2). 30 J

(3). 5 J

(4). 25 J

13. A mass m is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break when

(1).inclined at an angle of \(60^\circ\) from vertical

(2). the mass is at the highest point

(3). the wire is horizontal

(4). the mass is at the lowest point

14. A particle of mass 5m at rest suddenly breaks on its own into three fragments. Two fragments of mass m each move along mutually perpendicular direction with speed v each. The energy released during the process is

(1).\(\frac{3}{5}mv^2\)

(2). \(\frac{5}{3}mv^2\)

(3). \(\frac{3}{2}mv^2\)

(4). \(\frac{4}{3} mv^2\)

15. A moving block having mass m, collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of coefficientof restitution (e) will be

(1).0.5

(2). 0.25

(3). 0.8

(4). 0.4

16. A body initially rest and along a frictionless track from a height h (asshown in the figure) just completes a vertical circle of diameter AB = D.The height h is equal to

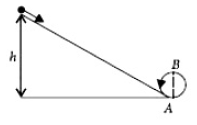
(1).\(\frac{3}{2} D\)

(2). \(D\)

(3). \(\frac{7}{5} D\)

(4). \(\frac{5}{4} D\)

17. Consider a drop of rain water having mass 1 g falling from a height of 1km. It hits the ground with a speed of 50ms⁻¹. Take 'g' constant with a value 10ms⁻².The work done by the (i) gravitational force and the (ii) resistive force of air is

(1).A. (i) 1.25 J (ii) -8.25 J

(2). B. (i) 100 J (ii) 8.75 J

(3). C. (i) 10 J (ii) -8.75 J

(4). D. (i) -10 J (ii) -8.25 J

18. A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 × 10⁻⁴J by the end of the second revolution after the beginning of the motion ?

(1).0.18 \(\frac{m}{s^2}\)

(2). 0.2\(\frac{m}{s^2}\)

(3). 0.1\(\frac{m}{s^2}\)

(4). 0.15\(\frac{m}{s^2}\)

19. A body of mass 1 kg begins to move under the action of time dependent force \(\vec{F}\) = \(\left(2t\hat{i} + 3t^2\hat{j}\right)\) N , where \(\hat{i}\) and \(\hat{j}\) are unit vectors along x and y axis.What power will developed by the force at the time t?

(1).(2t³ + 3t⁴) W

(2). (2t³ + 3t⁵) W

(3). (2t² + 3t³) W

(4). (2t² + 4t⁴b)

20. What is the minimum velocity with which a body of mass m must enter avertical loop of radius R so that can complete the loop?

(1).\(\sqrt{3gR}\)

(2). \(\sqrt{5gR}\)

(3). \(\sqrt{gR}\)

(4). \(\sqrt{2gR}\)

21. A bullet of mass 10 g moving horizontally with a velocity of 400ms⁻¹strikes a wood block of mass 2 kg which is suspended by light inextensible string of length 5 m. As a result, the centre of gravity of the block found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges out horizontally from the block will be

(1).100 ms⁻¹

(2). 80 ms⁻¹

(3). 120 ms⁻¹

(4). 160 ms⁻¹

22. Two identical balls A and B having velocities of 0.5ms⁻¹ and 0.3ms⁻¹ respectively collide elastically in one dimension. The velocities of B and A after the collision respectively will be

(1).−0.5 ms⁻¹ and 0.3 ms⁻¹

(2). 0.5 ms⁻¹ and −0.3 ms⁻¹

(3). −0.3 ms⁻¹ and 0.5 ms⁻¹

(4). 0.3 ms⁻¹ and 0.5 ms⁻¹

23. A particle moves from a point \(−2\hat{i} + 5\hat{j}\) to \(4\hat{j} + 3\hat{k}\) when a force of \(4\hat{i} + 3\hat{j}\) N is applied.How much work has been done by force ?

(1).8 J

(2). 11 J

(3). 5 J

(4). 2 J

24. Two particles A and B, move with constant velocities \(\vec{v_1}\) and \(\vec{v_2}\).At the initial moment their position vectors are \(\vec{r_1}\) and \(\vec{r_2}\) respectively. Thecondition for particles A and B for their collision is

(1).\(\vec{r_1}\) × \(\vec{v_1}\) = \(\vec{r_2}\) ×\(\vec{v_2}\)

(2). \(\vec{r_1}\) −\(\vec{r_2}\) =\(\vec{v_1}\) −\(\vec{v_2}\)

(3). \(\frac{\vec{r_1} −\vec{r_2}}{|\vec{r_1} −\vec{r_2}|}\)=\(\frac{\vec{v_2} −\vec{v_1}}{|\vec{v_2} −\vec{v_1}|}\)

(4). \(\vec{r_1}\) . \(\vec{v_1}\) = \(\vec{r_2}\) .\(\vec{v_2}\)

25. The heart of a man pumps 5 litres of blood through the arteries per minute at a pressure of 150 mm of mercury. If the density of mercury be13. × 10³kgm³ and g = 10ms² then the power of heart in watt is

(1).3.0

(2). 1.50

(3). 1.70

(4). 2.35

26. A ball is thrown vertically downwards from a height of 20 m with an initial velocity v₀.It collides with the ground, loses 50 percent of its energy in collision and rebounds to the same height. The initial velocity v₀ is (Take g = 10ms⁻²)

(1).28 ms⁻¹

(2). 10 ms⁻¹

(3). 14 ms⁻¹

(4). 20 ms⁻¹

27. On a frictionless surface, a block of mass M moving at speed v collides elastically with another block of same mass M which is initially at rest. After collision the first block moves at an angle 0 to its initial direction and has a speed v/3. The second block's speed after the collision

(1).\(\frac{3}{\sqrt{2}}\)v

(2). \(\frac{\sqrt{3}}{2}\)v

(3). \(\frac{2\sqrt{2}}{3}\)v

(4). \(\frac{3}{4}\)v

28. A particle of mass m is driven by a machine that delivers a constantpower k watts. If the particle starts from rest the force on the particle attime t is

(1).\({\sqrt{2mkt}}^{\frac{−1}{2}}\)

(2). \(\frac{1}{2}{\sqrt{mkt}}^{\frac{-1}{2}}\)

(3). \({\sqrt{\frac{mk}{2}t}}^{\frac{−1}{2}}\)

(4). \({\sqrt{mkt}}^{\frac{−1}{2}}\)

29. Two particles of masses m₁, m₂ move with initial velocities u₁ and u₂.On collision, one of the particles get excited to higher level, after absorbing energy e. If final velocities of particles be v₁ and v₂ then we must have

(1).\(\frac{1}{2}m_1{u_1}^2\) + \(\frac{1}{2}m_2{u_2}^2\) - \(\varepsilon\) = \(\frac{1}{2}m_1{v_1}^2\) + \(\frac{1}{2}m_2{v_2}^2\)

(2). \(\frac{1}{2}{m_1}^2{u_1}^2\) + \(\frac{1}{2}m_2{u_2}^2\) -+\(\varepsilon\) = \(\frac{1}{2}{m_1}^2{v_1}^2\) + \(\frac{1}{2}{m_2}^2{v_2}^2\)

(3). \({m_1}^2{u_1}\) + \({m_2}^2{u_2}\) - \(\varepsilon\) = \({m_1}^2{v_1}\) + \({m_2}^2{v_2}\)

(4). \(\frac{1}{2}m_1{u_1}^2\) + \(\frac{1}{2}m_2{u_2}^2\) = \(\frac{1}{2}m_1{v_1}^2\) + \(\frac{1}{2}m_2{v_2}^2\) - \(\varepsilon\)

30. Two similar springs P and Q have spring constants K_P and K_Q such that K_P > K_Q. They are stretched first by the same amount (case a),then by the same force (case b). The work done by the springs W_P and W_Q are related as, in case (a) and case (b) respectively

(1).W _P > W _Q; W _Q > W _P

(2). W _P < W _Q; W _Q < W _P

(3). W _P = W _Q; W _P > W _Q

(4). W _P = W _Q; W _P = W _Q

31. A body of mass (4m) is lying in x-y plane at rest. It suddenly explodesinto three pieces. Two pieces, each of mass (m) move perpendicular toeach other with equal speeds (v). The total kinetic energy generated dueto explosion is

(1).mv²

(2). 32mv²

(3). 2mv²

(4). 4mv²

32. Two bodies A and B of same mass undergo completely inelastic one dimensional collision. The body A moves with velocity v₁ while body B is at rest before collision. The velocity of the system after collision is v₂. The ratio v₁ : v₂ is

(1).1 : 2

(2). 2 : 1

(3). 4 : 1

(4). 1 : 4

33. A bob is whirled in a horizontal plane by means of a string with an initial speed of ω rpm.The tension in the string is T. If speed becomes 2ω while keeping the same radius, the tension in the string becomes:

(1).T

(2). 4T

(3). T/4

(4). \(\sqrt{2}\) T

34. A block of mass 10 Kg, moving in x-direction with a constant speed of \(10\, \text{ms}^{-1}\), is subjected to a retarding force
F = 0.1 x J/m during its travel from x = 20 m to 30 m. Its final KE will be

(1).475 J

(2). 450 J

(3). 275 J

(4). 250 J

35. A bob of heavy mass m is suspended by a light string of length l. The bob is given a horizontal velocity \(v_0\) as shown in the figure. If the string gets slack at some point P making an angle \(\theta\) from the horizontal, the ratio of the speed v of the bob at point P to its initial speed \(v_0\) is:

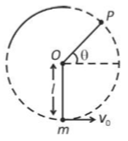
(1).\(\displaystyle \left(\frac{sin\theta}{2+3sin\theta}\right)^{\frac{1}{2}}\)

(2). \(\displaystyle \left(sin\theta \right)^{\frac{1}{2}}\)

(3). \(\displaystyle \left(\frac{1}{2+3sin\theta}\right)^{\frac{1}{2}}\)

(4). \(\displaystyle \left(\frac{cos\theta}{2+3sin\theta}\right)^{\frac{1}{2}}\)

36. The kinetic energies of two similar cars A and B are 100J and 225 J respectively. On applying breaks, car A stops after 1000 m and car B stops after 1500 m. If \(\text{F}_\text{A}\) and \(\text{F}_\text{B}\) are the forces applied by the breaks on cars A and B, respectively, then the ratio \(\text{F}_\text{A}\,/ \,\text{F}_\text{B}\) is

(1).\(\displaystyle \frac{1}{2}\)

(2). \(\displaystyle \frac{3}{2}\)

(3). \(\displaystyle \frac{2}{3}\)

(4). \(\displaystyle \frac{1}{3}\)