1. A bob is whirled in a horizontal circle by means of a string at an initial speed of 10rpm. If the tension in the string is quadrupled while keeping the radius constant, the new speed is:

(1).20 rpm

(2). 40 rpm

(3). 5 rpm

(4). 10 rpm

2. Let ω₁, ω₂ and ω₃ be the angular speed of the second hand, minute hand and hour hand of a smoothly running analog clock, respectively. If x₁, x₂ and x₃ are their respective angular distances in 1 minute then the factor which remains constant(k) is

(1).\( \frac{w_1}{x_1} \) = \( \frac{w_2}{x_2} \) = \( \frac{w_3}{x_3} \) = k

(2). \( w_1 x_1 \) = \( w_2 x_2 \) = \( w_3 x_3 \) = k

(3). \( w_1 x_1^2 \) = \( w_2 x_2^2 \) = \( w_3 x_3^2 \) = k

(4). \( w_1^2 x_1 \) = \( w_2^2 x_2 \) = \( w_3^2 x_3 \) = k

3. A ball is projected from point A with velocity 20m\( s^{−1} \) at an angle 60∘ to the horizontal direction. At the highest point B of the path (as shown in figure), the velocity vm \( s^{−1} \) of the ball will be:

(1).20

(2). 10\(\sqrt{3} \)

(3). Zero

(4). 10

4.

A particle is executing uniform circular motion with velocity \( \vec{v} \) and acceleration \( \vec{a} \). Which of the following is true?

(1). \( \vec{v} \) is a constant; \( \vec{a} \) is not constant

(2). \( \vec{v} \) is not a constant; \( \vec{a} \) is not a constant

(3). \( \vec{v} \) ia a constant; \( \vec{a} \) is a constant

(4). \( \vec{v} \) is not a constant; \( \vec{a} \) is a constant

5. A bullet is fired from a gun at the speed of 280m\( s^{−1} \) in the direction \( 30^\circ \) above the horizontal. The maximum height attained by the bullet is (g = 9.8m\( s^{−2} \), sin\( 30^\circ \) = 0.5)

(1).2000 m

(2). 1000 m

(3). 3000 m

(4). 2800 m

6. A ball is projected with a velocity, 10m\( s^{−1} \), at an angle of \( 60^\circ \) with the vertical direction. Its speed at the highest point of its trajectory will be

(1).Zero

(2). 5\(\sqrt{3} ms^{-1} \)

(3). 5 \(ms^{-1} \)

(4). 10 \(ms^{-1} \)

7. A cricket ball is thrown by a player at a speed of 20 m ∕ s in a direction \( 30^\circ \) above the horizontal. The maximum height attained by the ball during its motion is. (g = 10 m∕\(s^2 \) )

(1).25 m

(2). 5 m

(3). 10 m

(4). 20 m

8. If \(\vec{F}\) = 2\(\hat{i}\) + \(\hat{j}\) - \(\hat{k}\) and \(\vec{r}\) = 3\(\hat{i}\) + 2\(\hat{j}\) - 2\(\hat{k}\), then the scalar and vector products of \(\vec{F}\) and \(\vec{r}\) have the magnitudes respectively as

(1).10, 2

(2). 5, \(\sqrt{3}\)

(3). 4, \(\sqrt{5}\)

(4). 10, \(\sqrt{2}\)

9. A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution. If this particle were projected with the same speed at an angle ' θ ' to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by:

(1).\( \theta = {\cos^{-1} \left( \frac{gT^2}{\pi^2 R} \right)}^{1 / 2} \)

(2). \( \theta = {\cos^{-1} \left( \frac{\pi ^2R}{gT^2} \right)}^{1 / 2} \)

(3). \( \theta = {\sin^{-1} \left( \frac{\pi ^2R}{gT^2} \right)}^{1 / 2} \)

(4). \( \theta = {\sin^{-1} \left( \frac{2gT^2}{\pi^2 R} \right)}^{1 / 2} \)

10. The speed of a swimmer in still water is 20m ∕ s. The speed of river water is 10m ∕ s and is flowing due east. If he is standing on the south bank and wishes to cross the river along the shortest path, the angle at which he should make his strokes w.r.t. north is, given by

(1).\( 45^\circ \) west

(2). \( 30^\circ \) west

(3). \( 0^\circ \)

(4). \( 60^\circ \) west

11. When an object is shot from the bottom of a long smooth inclined plane kept at an angle \(60^\circ \) with horizontal, it can travel a distance \( {x_1} \) along the plane. But when the inclination is decreased to \(30^\circ \) and the same object is shot with the same velocity, it can travel \( {x_2} \) distance. Then \( {x_1}:{x_2} \) will be

(1).1 : \(2\sqrt{3} \)

(2). 1 : \(\sqrt{2} \)

(3). \(\sqrt{2} \) : 1

(4). 1 : \(\sqrt{3} \)

12. Two particles A and B are moving in uniform circular motion in concentric circles of radii r_A and r_B with speed v_A and v_B respectively. Their time period of rotation is the same. The ratio of angular speed of A to that of B will be

(1).1 : 1

(2). r_A : r_B

(3). v_A : v_B

(4). r_B : r_A

13. A particle starting from rest, moves in a circle of radius r. It attains a velocity of \( {V_0 m} \) m/s in the \( {n^{th}} \) round. Its angular acceleration will be

(1).\( \frac{V_0}{n} \) rad/ \( {s^2} \)

(2). \( \frac{V_0}{2 \pi \ nr^2} \) rad/ \( {s^2} \)

(3). \( \frac{V_0^2}{2 \pi \ nr^2} \) rad/ \( {s^2} \)

(4). \( \frac{V_0^2}{2 \pi \ nr} \) rad/ \( {s^2} \)

14. The x and y coordinates of the particle at any time are x = 5t − 2\(t^2 \) and y = 10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t = 2 s

(1).5m / \(s^2\)

(2). - 4m / \(s^2\)

(3). - 8m / \(s^2\)

(4). 0

15. If the magnitude of sum of two vectors is equal to the magnitude of difference of the two vectors, the angle between these vectors is:

(1).\( 45^\circ \)

(2). \( 180^\circ \)

(3). \( 0^\circ \)

(4). \( 90^\circ \)

16. A particle moves so that its position vector is given by \(\vec{r}\) = cos wt\(\hat{x}\) + sin wt\(\hat{y}\), where w is a constant. Which of the following is true ?

(1).Velocity is perpendicular to \(\vec{r}\) and acceleration is directed towards the origin

(2). Velocity is perpendicular to \(\vec{r}\) and acceleration is directed away from the origin

(3). Velocity and acceleration both are perpendicular to \(\vec{r}\)

(4). Velocity and acceleration both are parallel to \(\vec{r}\)

17. In the given figure, a = 15m\( s^{−2} \) represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R = 2.5 m at a given instant of time. The speed of the particle is

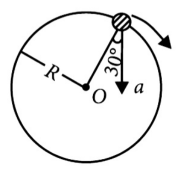
(1).4.5 m\(s^{-1} \)

(2). 5.0 m\(s^{-1} \)

(3). 5.7 m\(s^{-1} \)

(4). 6.2 m\(s^{-1} \)

18. If vectors \(\vec{A}\) = cos wt \(\hat{i}\) + sin wt\(\hat{j}\) and \(\vec{B}\) = cos \(\frac{wt}{2} \hat{i}\) + sin wt\(\hat{j}\) are functions of time, then the value of t at which they are orthogonal to each other is

(1).t = \( \frac{ \pi }{2}\)

(2). t = 0

(3). \( \frac{\pi } {4w}\)

(4). t = \( \frac{\pi } {2w}\)

19. The position vector of a particle \(\vec{R}\) as a function of time is given by \(\vec{R}\) = 4 sin\( \left(2\pi t\right)\hat{i}\) + 4 cos\( \left(2\pi t\right)\hat{j}\). Where R is in meters, t is in seconds and \(\hat{i}\) and \(\hat{j}\) denotes unit vectors along x - and y - directions, respectively. Which one of the following statements is wrong for the motion of particle

(1).Magnitude of velocity of particle is 8 metre/second

(2). Path of the particle is a circle of radius 4 metre

(3). Acceleration vector is along - \(\vec{R}\)

(4). Magnitude of acceleration vector is \(\frac{V^2}{R}\), where V is the velocity of particle

20. A projectile is fired from the surface of the earth with a velocity of 5 m\(s^{−1}\) and angle θ with horizontal. Another projectile fired from another planet with a velocity of 3 m\(s^{−1}\) at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is (in m\(s^{−2}\)) is (Given: g = 9.8m\(s^{−2}\))

(1).3.5

(2). 5.9

(3). 16.3

(4). 110.8

21. A particle is moving such that its position coordinates (x, y) are (2 m, 3 m) at time t = 0, (6 m, 7 m) at time t = 2 s and (13 m, 14 m) at time t = 5 s. Average velocity vector \(\vec{v}_{av}\) from t = 0 to t = 5 s is

(1).\(\frac{1}{5}\left(13\hat{i} + 14\hat{j}\right)\)

(2). \(\frac{7}{3}\left(\hat{i} + \hat{j}\right)\)

(3). \(2\left(\hat{i} + \hat{j}\right)\)

(4). \(\frac{11}{5}\left(\hat{i} + \hat{j}\right)\)

22. If | \(\vec{A}\) x \(\vec{B}\) | = \(\sqrt{3} \vec{A} . \vec{B}\) then the value of | \(\vec{A}\) + \(\vec{B}\) | is

(1).\({\left(A^2 + B^2 + AB\right)}^{1/2}\)

(2). \({\left(A^2 + B^2 + \frac{AB}{\sqrt{3}}\right)}^{1/2}\)

(3). \(A + B\)

(4). \({\left(A^2 + B^2 + \sqrt{3}AB\right)}^{1/2}\)

23. The vector sum of two forces is perpendicular to their vector differences. In that case, the forces

(1).Are equal to each other

(2). Are equal to each other in magnitude

(3). Are not equal to each other in magnitude

(4). Cannot be predicted

24. A particle moves along a circle of radius \(\left(\frac{20}{\pi}\right)\) m with constant quad tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is

(1).40 m / \(s^2\)

(2). 640\(\pi\) m / \(s^2\)

(3). 160\(\pi\) m / \(s^2\)

(4). 40\(\pi\) m / \(s^2\)

25. A particle A is dropped from a height and another particle B is projected in horizontal direction with speed of 5m ∕ sec from the same height then correct statement is

(1).Particle A will reach at ground first with respect to particle B

(2). Particle B will reach at ground first with respect to particle A

(3). Both particles will reach at ground simultaneously

(4). Both particles will reach at ground with same speed

26. An object of mass 3kg is at rest. Now a force of \(\vec{F}\) = 6\(t^2\hat{i} + 4t\hat{j}\) is applied on the object then velocity of object at t = 3s is

(1).\(18\hat{i} + 3\hat{j}\)

(2). \(18\hat{i} + 6\hat{j}\)

(3). \(3\hat{i} + 18\hat{j}\)

(4). \(18\hat{i} + 4\hat{j}\)

27. If | \(\vec{A} + \vec{B}\) | = | \(\vec{A}\) | + | \(\vec{B}\) | then angle between A and B will be

(1).\(90^\circ\)

(2). \(120^\circ\)

(3). \(0^\circ\)

(4). \(60^\circ\)

28. Two particles having mass M and m are moving in a circular path having radius R and r. If their time period are same then the ratio of angular velocity will be

(1).\(\frac{r}{R}\)

(2). \(\frac{R}{r}\)

(3). 1

(4). \(\sqrt{\frac{R}{r}}\)

29. Two projectiles of same mass and with same velocity are thrown at an angle of \(60^\circ\) and \(30^\circ\) with the horizontal, then which will remain same

(1).Time of flight

(2). Range of projectile

(3). Maximum height acquired

(4). All of them

30. A man is slipping on a frictionless inclined plane and a bag falls down from the same height. Then the velocity of both is related as

(1).\(V_B\) > \(V_m\)

(2). \(V_B\) < \(V_m\)

(3). \(V_B\) = \(V_m\)

(4). \(V_B\) and \(V_m\) can't be related

31. A 500 kg car takes a round turn of radius 50 m with a velocity of 36 km / hr. The centrepetal force is

(1).1000 N

(2). 750 N

(3). 250 N

(4). 1200 N

32. A person aiming to reach exactly opposite point on the bank of a stream is swimming with a speed of 0.5 m/s at an angle of \(120^\circ\) with the direction of flow of water. The speed of water in the stream, is

(1).0.25 m / s

(2). 0.5 m / s

(3). 1.0 m / s

(4). 0.433 m / s

33. Two racing cars of masses \(m_1\) and \(m_2\) are moving in circles of radii \(r_1\) and \(r_2\) respectively. Their speeds are such that each makes a complete circle in the same time t. The ratio of the angular speeds of the first to the second car is

(1).\(r_1\) : \(r_2\)

(2). \(m_1\) : \(m_2\)

(3). 1 : 1

(4). \(m_1 m_2\) : \(r_1 r_2\)

34. If a unit vector is represented by 0.5\(\hat{i}\) - 0.8\(\hat{j}\) + c\(\hat{k}\) then the value of c is

(1).\(\sqrt{0.01}\)

(2). \(\sqrt{0.11}\)

(3). 1

(4). \(\sqrt{0.39}\)

35. What is the value of linear velocity, if \(\vec{r}\) = 3\(\hat{i}\) - 4\(\hat{j}\) + \(\hat{k}\) and \(\vec{w}\) = 5\(\hat{i}\) - 6\(\hat{j}\) + 6\(\hat{k}\)

(1).4\(\hat{i}\) - 13\(\hat{j}\) + 6\(\hat{k}\)

(2). 18\(\hat{i}\) + 13\(\hat{j}\) - 2\(\hat{k}\)

(3). 6\(\hat{i}\) + 2\(\hat{j}\) - 3\(\hat{k}\)

(4). 6\(\hat{i}\) + 2\(\hat{j}\) + 8\(\hat{k}\)

36. Two particles A and B are connected by a rigid rod AB. The rod slides along perpendicular rails as shown here. The velocity of A to the left is 10 m / s. What is the velocity of B when angle \(\alpha\) = \(60^\circ\) ?

(1).10 m / s

(2). 9.8 m / s

(3). 5.8 m / s

(4). 17.3 m / s

37. A ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string will break if the tension is more thank 25 N. What is the miximum speed with which the ball can be moved ?

(1).5 m / s

(2). 3 m / s

(3). 14 m / s

(4). 3.92 m / s

38. Identify the vector quantity among the following

(1).Distance

(2). Angular momentum

(3). Heat

(4). Energy

39. A body is whirled in a horizontal circle of radius 20 cm. It has an angular velocity of 10 rad ∕ s. What is its linear velocity at any point on circular path?

(1).20 m ∕ s

(2). \(\sqrt{2}\) m ∕ s

(3). 10 m ∕ s

(4). 2 m ∕ s

40. The position vector of a particle is \(\vec{r}\) = (a cos wt)\(\hat{i}\) + (a sin wt)\(\hat{j}\). The velocity of the particle is

(1).Directed towards the origin

(2). Directed away from the origin

(3). Parallel to the position vector

(4). Perpendicular to the position vector

41. The angular speed of a flywheel making 120 revolutions / minute is

(1).4\(\pi \) rad / s

(2). 4\( {\pi}^2 \) rad / s

(3). \(\pi \) rad / s

(4). 2\(\pi \) rad / s

42. The angle between the two vectors \(\vec{A}\) = 3\(\hat{i}\) + 4\(\hat{j}\) + 5\(\hat{k}\) and \(\vec{B}\) = 3\(\hat{i}\) + 4\(\hat{j}\) - 5\(\hat{k}\)

(1).\(90^\circ\)

(2). \(180^\circ\)

(3). zero

(4). \(45^\circ\)

43. If a body A of mass M is thrown with velocity v at an angle of \(30^\circ\) to the horizontal and another body B of the same mass is thrown with the same speed at an angle of \(60^\circ\) to the horizontal, the ratio of horizontal range of A to B will be

(1).1: 3

(2). 1: 1

(3). 1 : \(\sqrt{3}\)

(4). \(\sqrt{3}\) : 1

44. The resultant of \(\vec{A}\) x 0 will be equal to

(1).Zero

(2). A

(3). Zero vector

(4). Unit vector

45. An electric fan has blades of length 30 cm measured from the axis of rotation. If the fan is rotating at 120 rpm, the acceleration of a point on the tip of the blade is

(1).\(1600\) \(m s^{−2}\)

(2). \(47.4\) \( m s^{−2}\)

(3). \(23.7\) \( m s^{−2}\)

(4). \(50.55\) \( m s^{−2}\)

46. The maximum range of a gun of horizontal terrain is 16 km. If g = 10 \(ms^{-2}\), then muzzle velocity of a shell must be

(1).\(160\) \(ms^{-1}\)

(2). \(200 \sqrt{2}\) \(ms^{-1}\)

(3). \(400\) \(ms^{-1}\)

(4). \(800\) \(ms^{-1}\)

47. A bus is moving on a straight road towards north with a uniform speed of 50 km ∕ hour then it turns left through \(90^\circ\). If the speed remains unchanged after turning, the increase in the velocity of bus in the turning process is

(1).70.7 km ∕ hour along south-west direction

(2). zero

(3). 50 km ∕ hour along west

(4). 70.7 km ∕ hour along north-west direction

48. The magnitude of vectors \(\vec{A}\), \(\vec{B}\), and \(\vec{C}\) are 3, 4, and 5 units respectively. If \(\vec{A}\) + \(\vec{B}\) = \(\vec{C}\) the angle between \(\vec{A}\) and \(\vec{B}\) is

(1).\(\frac{\pi }{2}\)

(2). \(cos^{-1}\left(0.6\right)\)

(3). \(tan^{-1}\left(\frac{7}{5}\right)\)

(4). \(\frac{\pi }{4}\)

49. A particle moving with uniform speed in a circular path maintains:

(1).Constant velocity

(2). Constant acceleration

(3). Constant velocity but varying acceleration

(4). Varying velocity and varying acceleration